How Handbells Helped an Advanced Math Student Get an A+
by Nikki Evans

Nikki Evans has been ringing with the JoyRingers at Pollard United Methodist Church in Tyler, Texas, since 2017, and solo ringing since 2018. She is a student at The University of Texas at Tyler, planning to graduate in May 2020. She has enjoyed studying the art of handbell ringing with the guidance of Jayne Brown, Arnold Sherman, and Sueda Luttrell.
I am a college student with a math major and a music minor. Many people think that’s a strange combination. Some tend to believe that math and music have little to nothing in common (even that they somehow use different halves of our brains), and many math people tend to believe that they aren’t creative. But what if math and music are a lot more alike than we tend to believe? What if we could use math to explain and create art and even music? This was my challenge in an abstract algebra class, and here is my story of how handbells saved the day in my classroom.
Abstract algebra discusses a lot of group theory. A group is some set defined under some operation and closed under the operation. The set must contain an identity element, each element of the set must contain an inverse in the set, and the associative property must hold. If all of these parameters are satisfied, then, indeed, you have a group, and group theory can then be applied.
This might sound intimidating in “math speak,” but we use group theory in everyday objects and tasks. Let’s look at the hours on a 12-hour clock as an example (ignoring minutes). The only possible numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12. After 12, it starts over again at 1. No matter how many hours you add, you will still end up with one of those twelve numbers. That means it is closed under addition. If it’s 3:00 now, in 12 hours, it will be 3:00 again (ignoring A.M. / P.M. designations). Our identity element is 12: you can add 12 to anything, and you will always get the same number you started with. You can also always figure out how long it will be until 12:00. For example, if it’s 3:00 now, it will be 12:00 in nine hours. For whatever hour you choose, you can know how long it is until 12:00 (and 12:00 is our identity element). In other words, each element of our set has an inverse (the element you add to get the identity, 12). If you start at 1:00 and add two hours, you will get 3:00. If you then add four hours, you get 7:00. You could also start at 1:00 and add 2+4 = 6 hours, and you will still end up at 7:00. This is the associative property. We see that this set is defined under addition, it is closed under addition, it has an identity, each element of the set has an inverse, and the associative property holds.
We can see that the hours on a clock meet all of the criteria stated above, so they mathematically qualify as a group. But who said a group had to be made up of numbers? It could be made of letters, or symbols — or even sounds. The Western twelve tone equal temperament scale that we use is made up of 12 possible notes (picture a piano octave from C to C including the black notes within it). Comparing these notes with the 12 numbers we discussed on the clock, think of C as 0 (since 12:00 functions like adding 0: the starting place), C#/Db as 1, D as 2, and so on. No matter what note you start on, you can move up or down by as many notes as you want, and you will still end up on one of our 12 notes (ignoring octave designations). Hence, we are closed under an operation (defining the distance between notes as the musical equivalent of addition). Let C be our identity element. No matter which note we’re on, we can know exactly how far it is from C. For example, D is two half steps above C, and Bb is two half steps below C. Reversing that thinking, we can also find an inverse for each element of our set (if you can go two half steps below C, you can also go two half steps above C). The associative property also holds, since transposing a note up by one half step and then transposing the result up two more half steps (for example) is the same as transposing the original note up three half steps. I imagine you are recalling some of your 8th grade algebra and wondering, “Okay, this math is nice, and I’m glad it’s related to music, but what does it have to do with handbells?”
I was struggling to pass abstract algebra when my professor assigned our final project. She gave us a list of ideas for topics, but allowed us to choose any topic that was beyond what we learned in class or an interesting real-life application of what we learned in class. We then had to do a 15-minute presentation for the rest of the class. My two worlds of math and music converged to create the perfect presentation. And that is how I ended up bringing handbells to an abstract algebra class.
For my project, I chose to cover applications of abstract algebra in music. Even when people do think about math and music, they tend to think narrowly of frequencies of sounds, adding intervals, and so on. In reality, the connections between music and math are abundant; we can’t even have sound without math, let alone music, yet few people seem to think beyond the basic math of measuring frequency or counting intervals.
For my 15-minute presentation, I didn’t have much time to dig very deep into this, but I did explain how the possible notes we have in music fit the mathematical definition of a group, which allows us to use group theory to describe music. Since the two groups I discussed earlier (the 12-hour clock and the 12-tone scale) function the same way, they have to share the same properties. That implies that they have to share the same subgroups as well. A subgroup is a group that is contained in another group. The group in the clock example has several subgroups. For example, the even numbers form a subgroup (the sum of any two even numbers is even, so they are closed under addition; the other criteria are satisfied like they were in earlier examples). So do multiples of three, multiples of four, and multiples of six.
Since those numbers function basically the same way as our 12 musical notes, what does that imply about music? The group of even numbers is made up of 0, 2, 4, 6, 8, and 10 (after that, 12 is the same as 0, 14 is the same as 2, and so on). Translating that to our previous definition of music notes, using half steps as our counting unit, this even-number group contains the notes C, D, E, F#/Gb, G#/Ab, A#/Bb, and C. This is the whole tone scale.
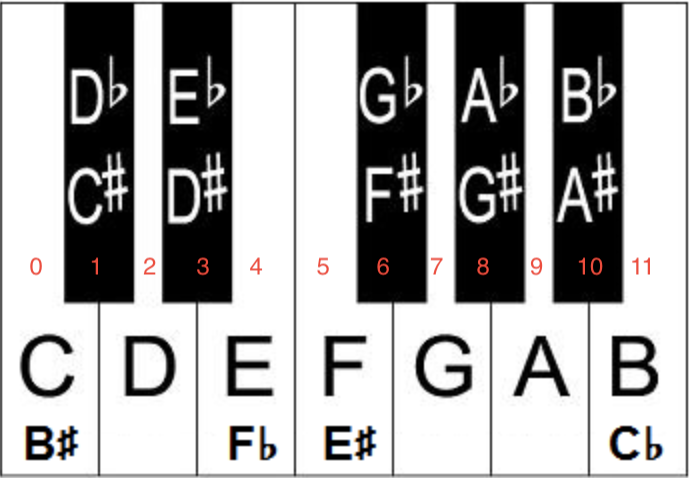
The multiples of three included in this group are 0, 3, 6, and 9. In music, this is C, D#/Eb, F#/Gb and A. If we keep the same notes and call them by different names, this is C, Eb, Gb, Bbb, which is a fully diminished seventh chord. The multiples of four are 0, 4, and 8. In music, that would be C, E, and G#, which is an augmented chord. The multiples of 6 are 0 and 6, or C and F#/Gb. This is the tritone (you may already know that it bisects the octave, and that it’s called the tritone because it’s three whole steps (six half steps)). All of these subgroups can be defined as multiples of some element in the group—in music’s case, particular notes in the 12-tone scale.
For my purposes of demonstrating those groups in a physical, tangible way, handbells were the perfect tool to clearly show the relationships in group theory. It was very convenient to have an instrument where the notes don’t have to be kept in a certain order, where I could easily pick up the notes I was talking about and show them to the class. I couldn’t do that with a guitar or any other instrument I had easy access to, so I brought some bells. My class had never seen handbells before, so they were fascinated by them, but the bells also did what I needed very well. I could physically separate the two possible whole tone scales from each other to show that they sounded basically the same, but didn’t share any notes in common (two discrete subgroups within the group), and I could pick up an augmented chord to show them what that sounded like. The audience could see and hear each note as it was played, personally experiencing group theory relationships in a real, physical way.
My presentation was warmly accepted. I received an A+ on the project, the highest grade in the class on the presentation part of it, and it brought me up a letter grade in the class. Even in the world of advanced math, handbells saved
the day.
I am a college student with a math major and a music minor. Many people think that’s a strange combination. Some tend to believe that math and music have little to nothing in common (even that they somehow use different halves of our brains), and many math people tend to believe that they aren’t creative. But what if math and music are a lot more alike than we tend to believe? What if we could use math to explain and create art and even music? This was my challenge in an abstract algebra class, and here is my story of how handbells saved the day in my classroom.
Abstract algebra discusses a lot of group theory. A group is some set defined under some operation and closed under the operation. The set must contain an identity element, each element of the set must contain an inverse in the set, and the associative property must hold. If all of these parameters are satisfied, then, indeed, you have a group, and group theory can then be applied.
This might sound intimidating in “math speak,” but we use group theory in everyday objects and tasks. Let’s look at the hours on a 12-hour clock as an example (ignoring minutes). The only possible numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12. After 12, it starts over again at 1. No matter how many hours you add, you will still end up with one of those twelve numbers. That means it is closed under addition. If it’s 3:00 now, in 12 hours, it will be 3:00 again (ignoring A.M. / P.M. designations). Our identity element is 12: you can add 12 to anything, and you will always get the same number you started with. You can also always figure out how long it will be until 12:00. For example, if it’s 3:00 now, it will be 12:00 in nine hours. For whatever hour you choose, you can know how long it is until 12:00 (and 12:00 is our identity element). In other words, each element of our set has an inverse (the element you add to get the identity, 12). If you start at 1:00 and add two hours, you will get 3:00. If you then add four hours, you get 7:00. You could also start at 1:00 and add 2+4 = 6 hours, and you will still end up at 7:00. This is the associative property. We see that this set is defined under addition, it is closed under addition, it has an identity, each element of the set has an inverse, and the associative property holds.
We can see that the hours on a clock meet all of the criteria stated above, so they mathematically qualify as a group. But who said a group had to be made up of numbers? It could be made of letters, or symbols — or even sounds. The Western twelve tone equal temperament scale that we use is made up of 12 possible notes (picture a piano octave from C to C including the black notes within it). Comparing these notes with the 12 numbers we discussed on the clock, think of C as 0 (since 12:00 functions like adding 0: the starting place), C#/Db as 1, D as 2, and so on. No matter what note you start on, you can move up or down by as many notes as you want, and you will still end up on one of our 12 notes (ignoring octave designations). Hence, we are closed under an operation (defining the distance between notes as the musical equivalent of addition). Let C be our identity element. No matter which note we’re on, we can know exactly how far it is from C. For example, D is two half steps above C, and Bb is two half steps below C. Reversing that thinking, we can also find an inverse for each element of our set (if you can go two half steps below C, you can also go two half steps above C). The associative property also holds, since transposing a note up by one half step and then transposing the result up two more half steps (for example) is the same as transposing the original note up three half steps. I imagine you are recalling some of your 8th grade algebra and wondering, “Okay, this math is nice, and I’m glad it’s related to music, but what does it have to do with handbells?”
I was struggling to pass abstract algebra when my professor assigned our final project. She gave us a list of ideas for topics, but allowed us to choose any topic that was beyond what we learned in class or an interesting real-life application of what we learned in class. We then had to do a 15-minute presentation for the rest of the class. My two worlds of math and music converged to create the perfect presentation. And that is how I ended up bringing handbells to an abstract algebra class.
For my project, I chose to cover applications of abstract algebra in music. Even when people do think about math and music, they tend to think narrowly of frequencies of sounds, adding intervals, and so on. In reality, the connections between music and math are abundant; we can’t even have sound without math, let alone music, yet few people seem to think beyond the basic math of measuring frequency or counting intervals.
For my 15-minute presentation, I didn’t have much time to dig very deep into this, but I did explain how the possible notes we have in music fit the mathematical definition of a group, which allows us to use group theory to describe music. Since the two groups I discussed earlier (the 12-hour clock and the 12-tone scale) function the same way, they have to share the same properties. That implies that they have to share the same subgroups as well. A subgroup is a group that is contained in another group. The group in the clock example has several subgroups. For example, the even numbers form a subgroup (the sum of any two even numbers is even, so they are closed under addition; the other criteria are satisfied like they were in earlier examples). So do multiples of three, multiples of four, and multiples of six.
Since those numbers function basically the same way as our 12 musical notes, what does that imply about music? The group of even numbers is made up of 0, 2, 4, 6, 8, and 10 (after that, 12 is the same as 0, 14 is the same as 2, and so on). Translating that to our previous definition of music notes, using half steps as our counting unit, this even-number group contains the notes C, D, E, F#/Gb, G#/Ab, A#/Bb, and C. This is the whole tone scale.

The multiples of three included in this group are 0, 3, 6, and 9. In music, this is C, D#/Eb, F#/Gb and A. If we keep the same notes and call them by different names, this is C, Eb, Gb, Bbb, which is a fully diminished seventh chord. The multiples of four are 0, 4, and 8. In music, that would be C, E, and G#, which is an augmented chord. The multiples of 6 are 0 and 6, or C and F#/Gb. This is the tritone (you may already know that it bisects the octave, and that it’s called the tritone because it’s three whole steps (six half steps)). All of these subgroups can be defined as multiples of some element in the group—in music’s case, particular notes in the 12-tone scale.
For my purposes of demonstrating those groups in a physical, tangible way, handbells were the perfect tool to clearly show the relationships in group theory. It was very convenient to have an instrument where the notes don’t have to be kept in a certain order, where I could easily pick up the notes I was talking about and show them to the class. I couldn’t do that with a guitar or any other instrument I had easy access to, so I brought some bells. My class had never seen handbells before, so they were fascinated by them, but the bells also did what I needed very well. I could physically separate the two possible whole tone scales from each other to show that they sounded basically the same, but didn’t share any notes in common (two discrete subgroups within the group), and I could pick up an augmented chord to show them what that sounded like. The audience could see and hear each note as it was played, personally experiencing group theory relationships in a real, physical way.
My presentation was warmly accepted. I received an A+ on the project, the highest grade in the class on the presentation part of it, and it brought me up a letter grade in the class. Even in the world of advanced math, handbells saved
the day.

Nikki Evans has been ringing with the JoyRingers at Pollard United Methodist Church in Tyler, Texas, since 2017, and solo ringing since 2018. She is a student at The University of Texas at Tyler, planning to graduate in May 2020. She has enjoyed studying the art of handbell ringing with the guidance of Jayne Brown, Arnold Sherman, and Sueda Luttrell.